2.4. Как убедиться в невозможности завершить вычисление?

2.4. Как убедиться в невозможности завершить вычисление?

 Мы установили, что вычисления могут как успешно завершаться, так и вообще не иметь конца. Более того, в тех случаях, когда вычисление завершиться в принципе не может, это его свойство иногда оказывается очевидным, иногда не совсем очевидным, а иногда настолько неочевидным, что ни у кого до сих пор не достало сообразительности однозначно такую невозможность доказать. С помощью каких методов математики убеждают самих себя и всех остальных в том, что такое-то вычисление не может завершиться? Применяют ли они при решении подобных задач какие-либо вычислительные (или алгоритмические) процедуры? Прежде чем мы приступим к поиску ответа на этот вопрос, рассмотрим еще один пример. Он несколько менее очевиден, чем (C), но все же гораздо проще (B). Возможно, нам удастся попутно получить некоторое представление о том, с помощью каких средств и методов математики приходят к своим выводам.

В предлагаемом примере участвуют числа, называемые шестиугольными:

1, 7, 19, 37, 61, 91, 127, …,

иными словами, числа, из которых можно строить шестиугольные матрицы (пустую матрицу на этот раз мы не включаем):

Каждое такое число, за исключением начальной единицы, получается добавлением к предыдущему числу соответствующего числа из ряда кратных 6:

6, 12, 18, 24, 30, 36, ….

Это легко объяснимо, если обратить внимание на то, что каждое новое шестиугольное число получается путем окружения предыдущего числа шестиугольным кольцом

причем число горошин в этом кольце обязательно будет кратно 6, а множитель при каждом увеличении шестиугольника на одно кольцо будет возрастать ровно на единицу.

Вычислим последовательные суммы шестиугольных чисел, увеличивая каждый раз количество слагаемых на единицу, и посмотрим, что из этого получится.

1 = 1, 1 + 7 = 8, 1 + 7 + 19 = 27, 1 + 7 + 19 + 37 = 64, 1 + 7 + 19 + 37 + 61 = 125.

Что же особенного в числах 1, 8, 27, 64, 125? Все они являются кубами. Кубом называют число, умноженное само на себя трижды:

1 = 1³ =1 ? 1 ? 1, 8 = 2³ = 2 ? 2 ? 2, 27 = 3³ = 3 ? 3 ? 3, 64 = 4³ = 4 ? 4 ? 4, 125 = 5³ = 5 ? 5 ? 5, ….

Присуще ли это свойство всем шестиугольным числам? Попробуем следующее число. В самом деле,

1 + 7 + 19 + 37 + 61 + 91 = 216 = 6 ? 6 ? 6 = 6³.

Всегда ли выполняется это правило? Если да, то никогда не завершится вычисление, необходимое для решения следующей задачи:

(E) Найти последовательную сумму шестиугольных чисел, начиная с единицы, не являющуюся кубом.

Думается, я сумею убедить вас в том, что это вычисление и в самом деле можно выполнять вечно, но так и не получить искомого ответа.

Прежде всего отметим, что число называется кубом не просто так: из соответствующего количества точек можно сложить трехмерный массив в форме куба (такой, например, как на рис. 2.1). Попробуем представить себе построение такого массива в виде последовательности шагов: вначале разместим где-нибудь угловую точку, а затем будем добавлять к ней, одну за другой, особые конфигурации точек, составленные из трех «плоскостей» — задней стенки, боковой стенки и потолка, как показано на рис. 2.2.

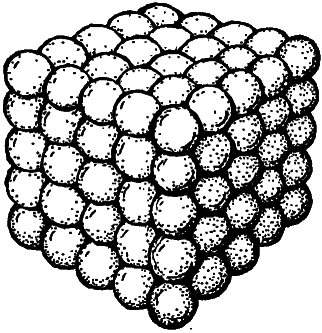
Рис. 2.1. Сферы, уложенные в кубический массив.

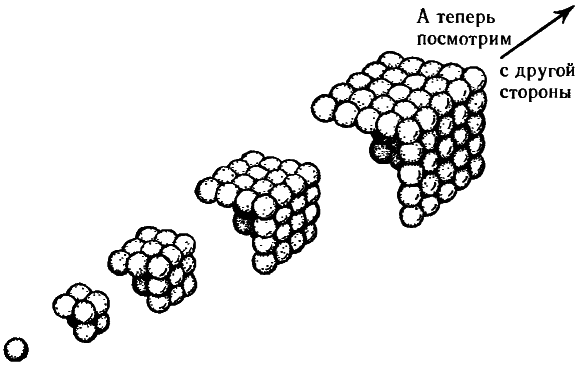
Рис. 2.2. Разберем куб на части — каждая со своей задней стенкой, боковой стенкой и потолком.

Посмотрим теперь на одну из наших трехгранных конфигураций со стороны, т. е. вдоль прямой, соединяющей начальную точку построения и точку, общую для всех трех граней. Мы увидим шестиугольник, подобный тому, что изображен на рис. 2.3. Точки, из которых складываются эти увеличивающиеся в размере шестиугольники, представляют собой, в сущности, те же точки, что образуют полный куб. То есть получается, что последовательное сложение шестиугольных чисел, начиная с единицы, всегда будет давать число кубическое. Следовательно, можно считать доказанным, что вычисление, требуемое для решения задачи (E), никогда не завершится.

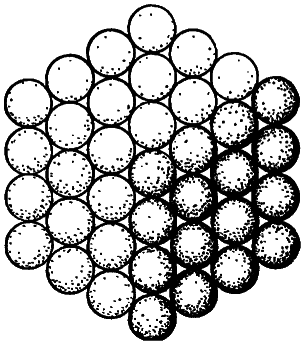
Рис. 2.3. Каждую часть построения можно рассматривать как шестиугольник.

Кто-то, быть может, уже готов упрекнуть меня в том, что представленные выше рассуждения можно счесть в лучшем случае интуитивным умозаключением, но не формальным и строгим математическим доказательством. На самом же деле, перед вами именно доказательство, и доказательство вполне здравое, а пишу все это я отчасти и для того, чтобы показать, что осмысленность того или иного метода математического обоснования никак не связана с его «формализованностью» в соответствии с какой-либо заранее заданной и общепринятой системой правил. Напомню, кстати, о еще более элементарном примере геометрического обоснования, применяемого для получения одного общего свойства натуральных чисел, — речь идет о доказательстве истинности равенства a ? b = b ? a, приведенном в §1.19. Тоже вполне достойное «доказательство», хотя формальным его назвать нельзя.

Представленное выше рассуждение о суммировании последовательных шестиугольных чисел можно при желании заменить более формальным математическим доказательством. В основу такого формального доказательства можно положить принцип математической индукции, т.е. процедуру установления истинности утверждения в отношении всех натуральных чисел на основании одного-единственного вычисления. По существу, этот принцип позволяет заключить, что некое положение P(n), зависящее от конкретного натурального числа n (например, такое: «сумма первых n шестиугольных чисел равна n³»), справедливо для всех n, если мы можем показать, во-первых, что оно справедливо для n = 0 (или, в нашем случае, для n = 1), и, во-вторых, что из истинности P(n) следует истинность и P(n+1). Думаю, нет необходимости описывать здесь в деталях, как можно с помощью математической индукции доказать невозможность завершить вычисление (E); тем же, кого данная тема заинтересовала, рекомендую попытаться в качестве упражнения выполнить такое доказательство самостоятельно.

Всегда ли для установления факта действительной незавершаемости вычисления достаточно применить некие четко определенные правила — такие, например, как принцип математической индукции? Как ни странно, нет. Это утверждение, как мы вскоре увидим, является одним из следствий теоремы Гёделя, и для нас крайне важно попытаться его правильно понять. Причем недостаточной оказывается не только математическая индукция. Недостаточным будет какой угодно набор правил, если под «набором правил» подразумевать некую систему формализованных процедур, в рамках которой возможно исключительно вычислительным путем проверить корректность применения этих правил в каждом конкретном случае. Такой вывод может показаться чересчур пессимистичным, ибо он, по-видимому, означает, что, несмотря на то, что вычисления, которые нельзя завершить, существуют, сам факт их незавершаемости строго математически установить невозможно. Однако смысл упомянутого следствия из теоремы Гёделя заключается вовсе не в этом. На самом деле, все не так уж и плохо: способность понимать и делать выводы, присущая математикам — как, впрочем, и всем остальным людям, наделенным логическим мышлением и воображением, — просто-напросто не поддается формализации в виде того или иного набора правил. Иногда правила могут стать частичной заменой пониманию, однако в полной мере такая замена не представляется возможной.