1.9. Невычислительные процессы

1.9. Невычислительные процессы

Из всех типов вполне определенных процессов, что приходят в голову, большая часть относится, соответственно, к категории феноменов, называемых мною «вычислительными» (имеются в виду, конечно же, «цифровые вычисления»). Возможно, читатель уже начал волноваться, что сторонники позиции C так и останутся у нас не при деле. Причем я еще ни словом не упоминал о строго случайных процессах, которые могут быть обусловлены, скажем, какими-либо исходными данными, получаемыми от квантовой системы. (О квантовой механике мы немного подробнее поговорим во второй части, главы 5 и 6.) Впрочем, для самой системы практически безразлично, подается на ее вход подлинно случайная последовательность данных или же всего лишь псевдослучайная, которую можно целиком и полностью сгенерировать вычислительным путем (см. §3.11). Действительно, несмотря на то, что между «случайным» и «псевдослучайным», строго говоря, существуют некоторые формальные отличия, они, на первый взгляд, не имеют непосредственного отношения к проблемам ИИ. Далее, в §3.11, §3.18 и последующих, я приведу некоторые серьезные доводы в пользу того, что «чистая случайность» и в самом деле абсолютно бесполезна для наших целей; если уж возникает такая необходимость, то лучше все же придерживаться псевдослучайности хаотического поведения, а все нормальные типы хаотического поведения, как уже подчеркивалось выше, относятся к категории «вычислительных».

А что нам известно о роли окружения? По мере развития каждого индивидуума у него или у нее формируется уникальное окружение, отличное от окружения любого другого человека. Возможно, именно это уникальное личное окружение и дает каждому из нас ту особенную последовательность входных данных, которая неподвластна вычислению? Хотя лично мне, например, сложно сообразить, на что именно в данном контексте может повлиять «уникальность» нашего окружения. Эти рассуждения напоминают разговор о хаосе, который мы вели выше (см. §1.7). Для обучения управляемого компьютером робота достаточно одной лишь модели некоего правдоподобного окружения (хаотического), при том, разумеется, условии, что в этой модели не будет ничего заведомо невычислимого. Роботу нет нужды учиться тем или иным навыкам в каком-то конкретном реальном окружении; его, разумеется, вполне устроит типичное окружение, моделирующее реальность вычислительными методами.

А может быть, численное моделирование пусть даже всего лишь правдоподобного окружения невозможно в принципе. Быть может, в окружающем физическом мире все же есть нечто такое, что на самом деле неподвластно численному моделированию. Возможно, некоторые сторонники A или B уже вознамерились приписать все не поддающиеся, на первый взгляд, вычислению проявления человеческого поведения невычислимости внешнего окружения. Должен, однако, заметить, что намерение это несколько опрометчиво. Ибо, как только мы признаем, что физическое поведение допускает где-то что-то такое, что невозможно моделировать вычислительными методами, мы тем самым тут же лишаемся главного, по всей видимости, основания сомневаться в правдоподобии, в первую очередь, самой точки зрения C. Если во внешнем окружении (т.е. вне мозга) имеют место процессы, не поддающиеся численному моделированию, то почему не могут оказаться таковыми и процессы, протекающие внутри мозга? В конце концов, внутренняя физическая организация мозга человека, по всей видимости, гораздо более сложна, чем большая часть (и это еще слабо сказано) его окружения, за исключением, быть может, тех его участков, где это окружение само оказывается под сильным влиянием деятельности других мозгов. Признание возможности внешней невычислимой физической активности лишает всякой силы главный аргумент против C. (См. также §3.9, §3.10.)

Следует сделать еще одно замечание относительно «не поддающихся вычислению» процессов, возможность существования которых предполагает позиция C. Под этим термином я имею в виду отнюдь не те процессы, которые всего-навсего невычислимы практически. Здесь, конечно же, уместно вспомнить и о том, что, хотя моделирование любого правдоподобного окружения, или же любое точное воспроизведение всех физических и химических процессов, протекающих в мозге, может быть, в принципе, вычислимым, на такое вычисление, скорее всего, понадобится столько времени или такой объем памяти, что вряд ли удастся выполнить его на любом реально существующем или даже вообразимом в ближайшем будущем компьютере. Вероятно, нереально даже написание соответствующей компьютерной программы, если учесть, какое огромное количество различных факторов придется принимать в расчет. Однако сколь бы существенными ни были все эти соображения (а мы еще вернемся к ним в §2.6, Q8 и §3.5), они не имеют никакого отношения к тому, что называю «невычислимостью» я (и чего требует C). Под «невычислимостью» я подразумеваю принципиальную невозможность вычисления в том смысле, который мы очень скоро обсудим. Вычисления, которые просто выходят за рамки существующих (или вообразимых) компьютеров или имеющихся в нашем распоряжении вычислительных методов, формально все равно остаются «вычислениями».

Читатель имеет полное право спросить: если ничего, что можно счесть «невычислимым», не обнаруживается ни в случайности, ни во влиянии окружения, ни в банальном несоответствии уровня сложности феномена нашим техническим возможностям, то что вообще я имею в виду, говоря «чего требует C»? В общем случае, это некий вид математически точной активности, невычислимость которой можно доказать. Насколько нам на данный момент известно, при описании физического поведения в подобной математической активности необходимости не возникает. Тем не менее, логически она возможна. Более того, она представляет собой нечто большее, нежели просто логическую возможность. Согласно приводимой далее в книге аргументации, возможность активности подобного общего характера прямо подразумевается физическими законами, несмотря на то, что ни с чем подобным в известной физике мы еще не встречались. Некоторые примеры такой математической активности замечательно просты, поэтому представляется вполне уместным проиллюстрировать с их помощью то, о чем я здесь говорю.

Начать мне придется с описания нескольких примеров классов хорошо структурированных математических задач, не имеющих общего численного решения (ниже я поясню, в каком именно смысле). Начав с любого из таких классов задач, можно построить «игрушечную» модель физической вселенной, активность которой (даже будучи полностью детерминированной) фактически не поддается численному моделированию.

Первый пример такого класса задач знаменит более остальных и известен под названием «десятая проблема Гильберта». Эта задача была предложена великим немецким математиком Давидом Гильбертом в 1900 году в составе этакого перечня нерешенных на тот момент математических проблем, которые по большей части определили дальнейшее развитие математики в начале (да и в конце) двадцатого века. Суть десятой проблемы Гильберта заключалась в отыскании вычислительной процедуры, на основании которой можно было бы определить, имеют ли уравнения, составляющие данную систему диофантовых уравнений, хотя бы одно общее решение.

Диофантовыми называются полиномиальные уравнения с каким угодно количеством переменных, все коэффициенты и все решения которых должны быть целыми числами. (Целые числа — это числа, не имеющие дробной части, например: …, -3, -2, -1, 0, 1, 2, 3, 4, …. Первым такие уравнения систематизировал и изучил греческий математик Диофант в третьем веке нашей эры.) Ниже приводится пример системы диофантовых уравнений:

6? + 2x² - y³ = 0, 5xy - z² + 6 = 0, ?² - ? + 2x - y + z - 4 = 0

Вот еще один пример:

6? + 2x² - y³ = 0, 5xy - z² + 6 = 0, ?² - ? + 2x - y + z - 3 = 0.

Решением первой системы является, в частности, следующее:

? = 1, x = l, у = 2, z = 4,

тогда как вторая система вообще не имеет решения (судя по первому уравнению, число у должно быть четным, судя по второму уравнению, число z также должно быть четным, однако это противоречит третьему уравнению, причем при любом ?, поскольку значение разности ?² - ? — это всегда четное число, а число 3 нечетно). Задача, поставленная Гильбертом, заключалась в отыскании математической процедуры (или алгоритма), позволяющей определить, какие системы диофантовых уравнений имеют решения (наш первый пример), а какие нет (второй пример). Вспомним (см. §1.5). что алгоритм — это всего лишь вычислительная процедура, действие некоторой машины Тьюринга. Таким образом, решением десятой проблемы Гильберта является некая вычислительная процедура, позволяющая определить, когда система диофантовых уравнений имеет решение.

Десятая проблема Гильберта имеет очень важное историческое значение, поскольку, сформулировав ее, Гильберт поднял вопрос, который ранее не поднимался. Каков точный математический смысл словосочетания «алгоритмическое решение для класса задач»? Если точно, то что это вообще такое — «алгоритм»? Именно этот вопрос привел в 1936 году Алана Тьюринга к его собственному определению понятия «алгоритм», основанному на изобретенных им машинах. Примерно в то же время другие математики (Черч, Клин, Гёдель, Пост и др.; см. [135]) предложили несколько иные процедуры. Как вскоре было показано, все эти процедуры оказались эквивалентными либо определению Тьюринга, либо определению Черча, хотя особый подход Тьюринга приобрел все же наибольшее влияние. (Только Тьюрингу пришла в голову идея специфической и всеобъемлющей алгоритмической машины, — названной универсальной машиной Тьюринга, — которая способна самостоятельно выполнить абсолютно любое алгоритмическое действие. Именно эта идея привела впоследствии к созданию концепции универсального компьютера, который сегодня так хорошо нам знаком.) Тьюрингу удалось показать, что существуют определенные классы задач, которые не имеют алгоритмического решения (в частности, «проблема остановки», о которой я расскажу ниже). Однако самой десятой проблеме Гильберта пришлось ждать своего решения до 1970 года, когда русский математик Юрий Матиясевич (представив доказательства, ставшие логическим завершением некоторых соображений, выдвинутых ранее американскими математиками Джулией Робинсон, Мартином Дэвисом и Хилари Патнэмом) показал невозможность создания компьютерной программы (или алгоритма), способной систематически определять, имеет ли решение та или иная система диофантовых уравнений. (См. [72] и [89], глава 6, где приводится весьма занимательное изложение этой истории.) Заметим, что в случае утвердительного ответа (т.е. когда система имеет-таки решение), этот факт, в принципе, можно констатировать с помощью особой компьютерной программы, которая самым тривиальным образом проверяет один за другим все возможные наборы целых чисел. Сколько-нибудь систематической обработке не поддается именно случай отсутствия решения. Можно, конечно, создать различные совокупности правил, которые корректно определяли бы, когда система не имеет решения (наподобие приведенного выше рассуждения с использованием четных и нечетных чисел, исключающего возможность решения второй системы), однако, как показывает теорема Матиясевича, список таких совокупностей никогда не будет полным.

Еще одним примером класса вполне структурированных математических задач, не имеющих алгоритмического решения, является задача о замощении. Она формулируется следующим образом: дан набор многоугольников, требуется определить, покрывают ли они плоскость; иными словами, возможно ли покрыть всю евклидову плоскость только этими многоугольниками без зазоров и наложений? В 1966 году американский математик Роберт Бергер показал (причем эффективно), что эта задача вычислительными средствами неразрешима. В основу его доводов легло обобщение одной из работ американского математика китайского происхождения Хао Вана, опубликованной в 1961 году (см. [176]). Надо сказать, что в моей формулировке задача оказывается несколько более громоздкой, чем хотелось бы, так как многоугольные плитки описываются в общем случае с помощью вещественных чисел (чисел, выражаемых в виде бесконечных десятичных дробей), тогда как обычные алгоритмы способны оперировать только целыми числами. От этого неудобства можно избавиться, если в качестве рассматриваемых многоугольников выбрать плитки, состоящие из нескольких квадратов, примыкающих один к другому сторонами. Такие плитки называются полиомино (см. [161]; [136], глава 13; [222]). На рис. 1.2 показаны некоторые плитки полиомино и примеры замощений ими плоскости. (Другие примеры замощений плоскости наборами плиток см. в НРК, с. 133-137, рис. 4.6-4.12.) Любопытно, что вычислительная неразрешимость задачи о замощении связана с существованием наборов полиомино, называемых апериодическими; такие наборы покрывают плоскость исключительно апериодически (т.е. так, что никакой участок законченного узора нигде не повторяется, независимо от площади покрытой плиткой плоскости). На рис. 1.3 представлен апериодический набор из трех полиомино (полученный из набора, обнаруженного Робертом Амманом в 1977 году; см. [176], рис. 10.4.11-10.4.13 на с. 555-556).

Математические доказательства неразрешимости с помощью вычислительных методов десятой проблемы Гильберта и задачи о замощении весьма сложны, и я, разумеется, не стану и пытаться приводить их здесь^{13}. Центральное место в каждом из этих доказательств отводится, в сущности, тому, чтобы показать, каким образом можно запрограммировать машину Тьюринга на решение задачи о диофантовых уравнениях или задачи о замощении. В результате все сводится к вопросу, который Тьюринг рассматривал еще в своем первоначальном исследовании: к вычислительной неразрешимости проблемы остановки — проблемы определения ситуаций, в которых работа машины Тьюринга не может завершиться. В §2.3 мы приведем несколько примеров явных вычислительных процедур, которые принципиально не могут завершиться, а в §2.5 будет представлено достаточно простое доказательство — основанное, по большей части, на оригинальном доказательстве Тьюринга, — которое, помимо прочего, показывает, что проблема остановки действительно неразрешима вычислительными методами. (Что же касается следствий из того самого «прочего», ради которого, собственно, и затевалось упомянутое доказательство, то на них, в сущности, построены рассуждения всей первой части книги.)

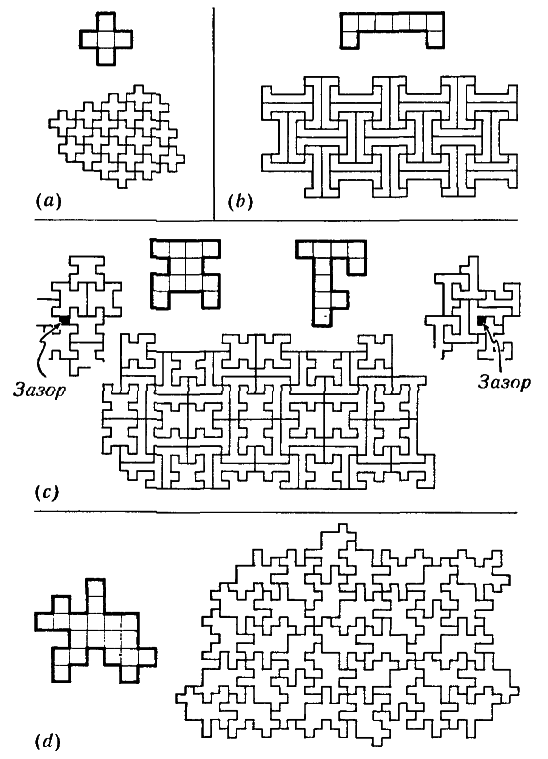
Рис. 1.2. Плитки полиомино и замощения ими бесконечной евклидовой плоскости (допускается использование зеркально отраженных плиток). Если брать полиомино из набора (с) по отдельности, то ни одно из них не покроет всю плоскость.

Рис. 1.З. Набор из трех полиомино, покрывающий плоскость апериодически (получен из набора Роберта Аммана).

Каким же образом можно применить такой класс задач, как задачи о диофантовых уравнениях или задачи о замощении, к созданию «игрушечной» вселенной, которая, будучи детерминированной, является, тем не менее, невычислимой? Допустим, что в нашей модели вселенной течет дискретное время, параметризованное натуральными (т.е. целыми неотрицательными) числами 0, 1, 2, 3, 4, …. Предположим, что в некий момент времени n состояние вселенной точно определяется одной задачей из рассматриваемого класса, скажем, набором полиомино. Необходимо установить два вполне определенных правила относительно того, какой из наборов полиомино будет представлять состояние вселенной в момент времени n + 1 при заданном наборе полиомино для состояния вселенной в момент времени n, причем первое из этих правил применяется в том случае, если полиомино покрывают всю плоскость без зазоров и наложений, а второе — если это не так. То, как именно будут выглядеть подобные правила, не имеет в данном случае особого значения. Можно составить список S₀, S₁, S₂, S₃, S₄, S₅, … всех возможных наборов полиомино таким образом, чтобы наборы, содержащие в общей сложности четное число квадратов, имели бы четные индексы S₀, S₂, S₄, S₆, …, а наборы с нечетным количеством квадратов — нечетные индексы S₁, S₃, S₅, S₇, …. (Составление такого списка не представляет особой сложности; нужно лишь подобрать соответствующую вычислительную процедуру.) Итак, «динамическая эволюция» нашей игрушечной вселенной задается теперь следующим условием:

Из состояния S_n в момент времени t вселенная переходит в момент времени t + 1 в состояние S_n+1, если набор полиомино S_n покрывает плоскость, и в состояние S_n+2, если набор S_n не покрывает плоскость.

Поведение такой вселенной полностью детерминировано, однако поскольку в нашем распоряжении нет общей вычислительной процедуры, позволяющей установить, какой из наборов полиомино Sn покрывает плоскость (причем это верно и тогда, когда общее число квадратов постоянно, независимо от того, четное оно или нет), то невозможно и численное моделирование ее реального развития. (См. рис. 1.4.)

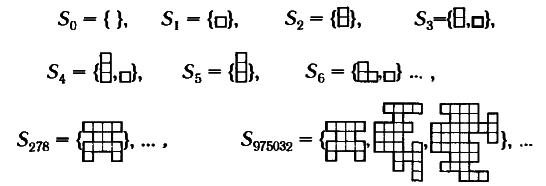
Рис. 1.4. Невычислимая модель «игрушечной» вселенной. Различные состояния этой детерминированной, но невычислимой вселенной даны в виде возможных конечных наборов полиомино, пронумерованных таким образом, что четные индексы S_n соответствуют четному общему количеству квадратов в наборе, а нечетные индексы — нечетному количеству квадратов. Временная эволюция происходит в порядке увеличения индекса (S₀, S₂, S₃, S₄, …, S₂₇₈, S₂₈₀, …), при этом индекс пропускается, когда предыдущий набор оказывается не в состоянии замостить плоскость.

Безусловно, такую схему нельзя воспринимать хоть сколько-нибудь всерьез — она ни в коем случае не моделирует реальную вселенную, в которой все мы живем. Эта схема приводится здесь (как, собственно, и в НРК, с. 170) для иллюстрации того часто недооцениваемого факта, что между детерминизмом и вычислимостью существует вполне определенная разница. Некоторые полностью детерминированные модели вселенной с четкими законами эволюции невозможно реализовать вычислительными средствами. Вообще говоря, как мы убедимся в §7.9, только что рассмотренные мною весьма специфические модели не совсем отвечают реальным требованиям точки зрения C. Что же касается тех феноменов, которые отвечают-таки этим самым реальным требованиям, и некоторых связанных с упомянутыми феноменами поразительных физических возможностях, то о них мы поговорим в §7.10.