Отрицательные и положительные величины

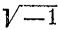. Отрицательные величины алгебры реальны лишь постольку, поскольку они относятся к положительным величинам, реальны лишь в своих отношениях к последним; взятые вне этого отношения, сами по себе, они мнимы. В тригонометрии и аналитической геометрии, вместе с построенными на них отраслями высшей математики, они выражают определенное направление движения, противоположное положительному направлению. Но можно с одинаковым успехом отсчитывать синусы и тангенсы как в первом, так и в четвертом квадратах и значит можно обратить плюс в минус. Точно так же в аналитической геометрии можно отсчитывать абсциссы в круге, либо начиная с периферии, либо начиная с центра и вообще у всех кривых в направлении, обозначаемом обыкновенно минусом, и при этом мы получаем правильное рациональное уравнение кривой. Здесь + существует только как дополнение -, и обратно. Но алгебра в своих абстракциях рассматривает их как действительные, самостоятельные величины, без отношения к какой-нибудь большей, положительной величине. (Энгельс, Диалектика природы, стр. 111, 1932 г.)