1. Преобразование суждений

1. Преобразование суждений

Преобразование простых атрибутивных суждений. Простые атрибутивные суждения, заключая в себе определенный смысл, сами по себе не раскрывают полностью всей гаммы содержащихся в них взаимоотношений между их субъектом и предикатом, количеством и качеством. Например, известно, что «Все поэты — впечатлительные люди». Но «Все ли впечатлительные люди непременно поэты»? Перефразируя известную шутку: «Чтобы сделать рагу из зайца, надобно иметь, как минимум, кошку», спросим себя: «Чтобы числиться по разряду поэтов, достаточно ли слыть впечатлительным человеком?»

Для выяснения точного логического смысла суждения нередко требуется преобразование его формы. Это достигается прежде всего посредством таких логических операций, как обращение, превращение, противопоставление субъекту и противопоставление предикату.

Обращение. Это преобразование суждения путем перестановки его субъекта и предиката местами. При этом количество суждения (кванторное слово) может изменяться, а качество не меняется.

Какие здесь действуют закономерности? Их три:

а) общеутвердительное суждение (А) преобразуется в частноутвердительное (I). Обусловлено это тем, что субъект в нем распределен, а предикат, как правило, не распределен. Формула обращения: «Все S есть Р» — «Некоторые Р есть S». Так, в суждении «Все адвокаты — юристы» поставим субъект на место предиката, а предикат на место субъекта. В результате получим: «Некоторые юристы — адвокаты» (ибо юристами, как отмечалось, являются не только адвокаты, но и прокуроры, судьи, следователи и др.). Это графически можно представить так:

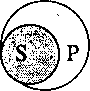
где S — адвокаты, Р — юристы.

Такое преобразование называется «обращение с ограничением». Исключение составляет обращение общеутвердительных выделяющих суждений, в которых и субъект и предикат распределены. Они обращаются в общеутвердительные же. Это «чистое обращение». Формула: «Все S (и только S) есть Р» — «Все Р есть S». Например: «Все люди — разумные существа» — «Все разумные существа — люди». Это видно на круговой схеме:

Все правильные определения, поскольку в них объем определяющего равен объему определяемого (правило соразмерности), тоже допускают лишь чистое обращение;

б) частноутвердительное суждение (I) обращается в частноутвердительное (I). Субъект и предикат в них, как правило, не распределены. Формула обращения: «Некоторые S есть Р» — «Некоторые Р есть S». Пример: «Некоторые юристы — депутаты Государственной Думы» — «Некоторые депутаты Государственной Думы — юристы». На круговой схеме:

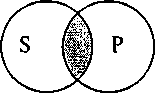
Исключение составляют суждения, в которых субъект не распределен, а предикат распределен. В этих случаях частноутвердительное суждение преобразуется в общеутвердительное. Формула: «Некоторые S (и только S) есть Р». — «Все Р есть S». Пример: «Некоторые преступники — убийцы» — «Все убийцы — преступники». Это «обращение с приращением». Графически:

в) общеотрицательное суждение (Е) обращается в общеотрицательное (Е), так как субъект и предикат здесь распределены. Формула: «Ни одно S не есть Р» — «Ни одно Р не есть S». Например: «Ни один свидетель не явился в суд» — «Ни один явившийся в суд не свидетель».

Частноотрицательные суждения не обращаются. Субъект в них не распределен, следовательно, он не может стать предикатом нового, тоже отрицательного суждения, где предикат всегда распределен. Попробуем для примера выяснить, что произойдет с суждением «Некоторые мужчины — не женатые». Означает ли оно, что «Ни один женатый — не мужчина»? Или только «некоторые»? И тот и другой вывод бессмысленны. А иного сделать нельзя. Это видно на схеме:

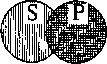
Какое значение имеет такая логическая операция, как обращение, в практике мышления? Благодаря ей полнее раскрываются взаимоотношения между субъектом и предикатом суждения, а следовательно, связи и отношения между предметами мысли, отражаемыми в суждении. С субъекта, четко выраженного кванторным словом, наш взор переносится на предикат, который становится субъектом, а следовательно, обретает свое кванторное слово. Вспомним наши утверждения: «Всякое понятие выражается в слове, но не всякое слово выражает понятие» или «Всякое суждение есть предложение, но не всякое предложение есть суждение». Обращение может принимать и не столь развернутую, полную форму. Примером сокращенного обращения может служить пословица: «Не все то золото, что блестит». Очевидно, это результат обращения суждения: «Все то, что золото, блестит» (но «Не все то, что блестит, — золото»). С помощью обращения проверяется правильность определений. Если после перестановки определяемого и определяющего смысл определения не меняется, значит, оно правильное. Нетрудно понять, что эту операцию можно производить и в юридической практике, когда требуется более точно выявить соотношения между теми или иными понятиями. Например: «Всякий закон есть нормативный правовой акт», но «Не всякий нормативный правовой акт есть закон» (есть еще указы, инструкции, правила и т. п.). Обращение играет незаменимую роль в проверке правильности юридических определений, от которых требуется особая точность.

Превращение. Это преобразование суждения путем перемены его качества на противоположное. Количество суждения, его субъект и предикат при этом не меняются.

В превращении проявляются следующие закономерности:

а) общеутвердительное суждение (А) преобразуется в общеотрицательное (Е). Формула превращения: «Все S есть Р» — «Ни одно S не есть не-Р». Так, суждение: «Все адвокаты — юристы» по качеству утвердительное. Превращаем его в отрицательное, но так при этом, чтобы его смысл не изменился: «Ни один адвокат не является неюристом». Вот графическое изображение:

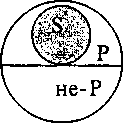
б) общеотрицательное суждение (Е), наоборот, превращается в общеутвердительное (А). Формула: «Ни одно S не есть не-Р» — «Все S есть Р». Пример: «Ни одно преступление не осталось нераскрытым» — «Все преступления раскрыты». Графически:

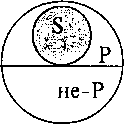
в) частноутвердительное суждение (I) превращается в частноотрицательное (О). Формула: «Некоторые S есть Р» — «Некоторые S не есть не-Р». Пример: «Некоторые свидетели дали верные показания» — «Некоторые свидетели не дали неверных показаний». Графически:

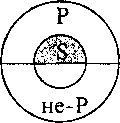
г) частноотрицательное суждение (О) превращается в частноутвердительное (I). Формула: «Некоторые S не есть Р» — «Некоторые S есть не-Р». Например: «Некоторые книги не есть интересные» — «Некоторые книги есть неинтересные». Графически:

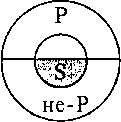
Значение превращения как логической операции состоит в том, что благодаря ему в суждении раскрывается новый, более богатый смысл: утверждение принимает форму отрицания и наоборот. Представим себе спор нескольких людей. Один говорит: «Петров — патриот». Другой возражает: «Петров — не патриот». Находится третий, который возражает второму: «Петров не является непатриотом». Высказанное им суждение и есть пример превращения. С одной стороны, оно равнозначно первому: двойное отрицание равно утверждению: «Петров — патриот», а с другой — противоположно суждению: «Петров — не патриот».

В юридических дискуссиях, спорах и т.д. подобный прием используется нередко. О нем свидетельствуют, в частности, выражения типа: «не есть не ...», «не является не ...» и др.

Обращение и превращение выступают основными, исходными логическими операциями с суждениями. Их различное сочетание порождает еще две операции: противопоставление субъекту и противопоставление предикату, которые считаются производными или смешанными.

Противопоставление субъекту. Так называется преобразование суждения путем обращения и последующего превращения. Приведем для краткости лишь один пример. Если суждение: «Все адвокаты — юристы» сначала обратим в суждение: «Некоторые юристы — адвокаты», а это последнее, в свою очередь, превратим в суждение: «Некоторые юристы не есть неадвокаты» (хотя есть и прокуроры, и судьи, и др.), то получим противопоставление субъекту. Предикат заключительного суждения — «неадвокаты» противопоставляется субъекту исходного суждения — «адвокаты». Отсюда название самой операции.

Противопоставление предикату. Это преобразование суждения путем превращения и последующего обращения. Пример. Суждение: «Все адвокаты — юристы» сначала превратим в суждение: «Ни один адвокат не является неюристом», а это последнее обратим в суждение: «Ни один неюрист не является адвокатом» (попросту говоря, среди неюристов адвокатов искать не следует). Получается, что предикату исходного суждения «юристы» мы противопоставили понятие «неюристы» и сделали его субъектом нового суждения. Этим объясняется название операции.

Значение двух последних операций, поскольку они носят производный, смешанный характер, слагается из значения исходных, основных, т.е. они позволяют извлечь дополнительную информацию, заложенную в преобразуемом суждении, раскрыть новые его грани и оттенки.

Преобразование простых реляционных суждений. Как и суждения о свойствах чего-либо, реляционные суждения (или суждения об отношениях между предметами) могут подвергаться тем же основным преобразованиям — обращению или превращению и с той же целью уточнения их логического смысла. Однако здесь неизбежны некоторые особенности, обусловленные особенностями самих суждений об отношениях. Для преобразования такого рода суждения прежде всего необходимо знать свойства выражаемого им отношения — является ли оно симметричным или несимметричным, рефлексивным или нерефлексивным, транзитивным или нетранзитивным.

Обращение. Если отношение симметрично, обращение реляционного суждения будет сводиться к простой перестановке местами членов отношения х и у. Причем само отношение R остается тем же. Например: «В. Маяковский — современник М. Горького» — «М. Горький — современник В. Маяковского». Другие примеры: «СНГ не равно СССР» — «СССР не равен СНГ»; «Нормы права подобны нормам морали» — «Нормы морали подобны нормам права». Если же отношение несимметрично, то обращение предполагает не только перестановку местами х и у, но и замену самого отношения R на обратное. Примеры: «М. Горький родился раньше Л. Леонова» — «Л. Леонов родился позже М. Горького»; «Рязань восточнее Москвы» — «Москва западнее Рязани»; «Земля больше Луны» — «Луна меньше Земли». Важно при этом обращать внимание на то, чтобы смысл суждения оставался одним и тем же: меняться должна лишь его логическая форма. Естественно, что в таком случае суждения оказываются синонимичными, поэтому в процессе рассуждения их можно заменять одно на другое. Так, если «Мораль возникла раньше права», то равнозначным ему будет суждение «Право возникло позже морали».

Если отношение транзитивно или нетранзитивно, то обращение принимает соответственно несколько иной вид. В случае транзитивности обращение суждения предполагает замену отношения на обратное. Так, если «Солнце больше Земли, а Земля больше Луны», то «Солнце больше Луны». Отсюда «Луна меньше Солнца». В случае же нетранзитивности обращение требует не только замены отношения на обратное, но и предварительного подбора соответствующего отношения. Так, если «Отец моего отца мне не отец, а дед», то «Я не сын ему, а внук».

Превращение. Применительно к реляционным суждениям оно тоже обладает своеобразием. Так, в случае симметричности отношения утвердительное суждение превращается в отрицательное (разумеется, с двойным отрицанием, иначе смысл суждения изменится на прямо противоположный, и, следовательно, это будет уже другое суждение). Например: «В. Маяковский — современник М. Горького» — «В. Маяковский не может быть не современником М. Горького». В случае же несимметричности отношения утвердительное суждение непросто становится отрицательным, а предполагает замену отношения на обратное. Например: «М. Горький родился раньше Л. Леонова» — «М. Горький родился (во всяком случае) не позже Л. Леонова». Естественно, что такие суждения тоже синонимичны, а следовательно, в практике мышления могут меняться одно на другое.

Следует лишь учитывать относительный характер этой синонимичности. Так, в результате превращения может меняться модальность суждения, оно может приобретать дополнительный смысл, не заложенный в исходном суждении и т. д.

Нетрудно понять, что если возможны обращение и превращение реляционных суждений, то на этой основе возможны и другие, производные и смешанные формы преобразования подобных суждений.

Преобразование сложных суждений. Сложные суждения, образованные из простых или других сложных суждений с помощью логических союзов, могут тоже подвергаться преобразованиям. Выше отмечалось, что одно и то же по смыслу сложное суждение может быть выражено в различной логической форме — конъюнкции, дизъюнкции, импликации и т. д. Это означает, что эквивалентность (равносильность, равнозначность) подобных суждений делает возможным производить над ними различные логические операции — преобразовывать их друг в друга, выражать одно через другое. Вот лишь некоторые из таких преобразований:

а) конъюнкция может быть выражена через дизъюнкцию, а именно: отрицание конъюнкции эквивалентно дизъюнкции отрицаний. Формула такого преобразования: ?(A?B)??A??B. Например: «Неверно, что Петров адвокат и в то же время судья». Это равнозначно суждению: «Петров не адвокат или он не судья». Обратим внимание, что дизъюнкция здесь не исчерпывающая. Поэтому может быть так, что Петров и не адвокат, и не судья, а например, прокурор;

б) дизъюнкция может быть выражена через конъюнкцию: отрицание дизъюнкции эквивалентно конъюнкции отрицаний. Формула ?(A?B)??A??B. Например: «Неверно, что Петров изучал логику в вузе или что он изучал ее самостоятельно». Это равносильно суждению: «Петров не изучал логики в вузе, и он не изучал ее самостоятельно»;

в) импликация может быть выражена через конъюнкцию: импликация эквивалентна отрицанию конъюнкции антецедента (основания) и ложного консеквента (следствия). Формула: А ? В ? ?(А??В). Пример: «Если Петров юрист, то он знает логику». Это равноценно суждению: «Неверно, что Петров юрист и он не знает логики»;

г) импликация может быть выражена через дизъюнкцию: импликация эквивалентна дизъюнкции ложного антецедента и консеквента. Формула: А ? В ? ?А?В). Пример: «Если Петров адвокат, то он имеет специальное, юридическое образование» — «Или Петров не адвокат, или он имеет специальное, юридическое образование».

Конъюнкция и дизъюнкция, в свою очередь, могут быть выражены через импликацию. Возможны и иные, самые разнообразные преобразования сложных суждений в другие. Важно при этом учитывать, что в процессе преобразования может меняться лишь логическая форма сложного суждения, его логический союз. Что же касается смысла самого суждения, то он должен оставаться тем же самым. В противном случае это будет уже новое суждение с иным смыслом.

Как же устанавливается эквивалентность суждений? Это достигается с помощью таблиц истинности. Так, если мы сравним таблицы истинности конъюнкции и (слабой) дизъюнкции (см. выше), то заметим, что сложное суждение конъюнкции А?В истинно только тогда, когда истинны оба исходных суждения А и В; а суждение дизъюнкции A?B ложно только в том случае, когда ложны как А, так и В. Следовательно, логические союзы конъюнкции ? и дизъюнкции ? находятся, можно сказать, в обратной зависимости. Учитывая это, конъюнкцию можно выразить через дизъюнкцию, а дизъюнкцию через конъюнкцию. При этом получаются именно эквивалентные формы, т. е. такие, которые истинны и ложны при тех же значениях составляющих их суждений.

Установление подобных эквивалентностей с помощью таблиц истинности открывает возможность, уже не обращаясь всякий раз непосредственно к сопоставлению самих таблиц, преобразовывать одни суждения в другие.

Для чего это нужно? Благодаря замене одних суждений другими, эквивалентными им, можно упрощать сложные рассуждения, используя одни логические союзы вместо других. Так, в любом, самом сложном суждении можно, пользуясь правилом замены одних логических союзов другими, устранить все знаки, кроме только знаков конъюнкции и отрицания, или лишь дизъюнкции и отрицания, или же импликации и отрицания. Этим обстоятельством широко пользуются в символической логике — прежде всего в логике высказываний.