3. Неполная индукция
3. Неполная индукция
Неполной индукцией называется умозаключение обо всем классе предметов в целом на основе изучения лишь части предметов данного класса.
Формула неполной индукции:
S1 — P
S2 — P
…..
Sn — P
S1, S2 ... Sn ... составляют часть класса S.
Следовательно, все S — Р.
В символической записи:
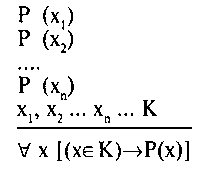
Посредством неполной индукции преодолевается недостаток полной индукции. Она применяется прежде всего там, где число элементов исследуемого класса неопределенно, неограниченно или бесконечно. Таковы так называемые «открытые классы». Правда, она может применяться и там, где это число ограниченно и его нетрудно сосчитать («закрытые классы»), однако надобности в исследованиях всех без исключения элементов почему-либо нет. Так была установлена, например, электропроводность металлов на основе знания лишь о некоторых металлах, хотя число их определенно.
Возможность заключения в форме неполной индукции обусловлена тем, что если некоторое общее свойство принадлежит более или менее значительной части класса, то в силу его большей или меньшей существенности оно может принадлежать и всему классу в целом.
Познавательное значение неполной индукции по сравнению с полной в известном смысле более важно и велико. Как отмечалось, в полной индукции заключение не распространяется на другие предметы, кроме изученных, хотя весь их класс в целом и рассматривается с новой стороны. В заключении же неполной индукции осуществляется логический перенос знания с изученной части класса на всю остальную его часть.
Однако в этом достоинстве неполной индукции содержится и ее существенный недостаток. В отличие от полной индукции сам вывод здесь — даже при истинности всех посылок — может давать в принципе лишь вероятное знание, способное в большей или меньшей степени приближаться к достоверному. Обобщение, содержащееся в нем, может обеспечивать и твердое, достоверное знание, но лишь в том случае, если оно облекается в форму частного суждения. Однако кванторное слово — по сравнению с полной индукцией — употребляется здесь в ином смысле: «Некоторые, а может быть и все». Следовательно, сами такие обобщения носят характер неопределенного частного суждения.
Неполная индукция имеет две основные разновидности: это популярная индукция и научная индукция.
Популярная индукция (или индукция через простое перечисление). Ее полное наименование: «индукция через простое перечисление, когда не встречается противоречащий случай» («inductio per enumerationem simplicem, ubi non reperitur instantia contradictoria»). Повседневная жизнь людей дает массу примеров такой индукции. Так, люди не раз наблюдали, что ласточки перед дождем летают низко над землей. На этой основе был сделан вывод: «Всегда ласточки перед дождем летают низко над землей». Подобных примет, сделанных на основе непосредственных наблюдений, зафиксировано народной мудростью немало. Вот почему они получили название «народные приметы», а сама индукция — наименование «популярная» («народная»). Однако такие выводы носят характер лишь вероятного знания. Достаточно встретиться противоречащему случаю, чтобы заключение оказалось ложным. Вспомним классическую историю с лебедями. На основе бесчисленных наблюдений издавна был сделан вывод, что «Все лебеди белы». Однако со временем в Австралии были обнаружены черные лебеди, которых теперь можно видеть и в других местах. То же самое с выводом: «Все березы белы». Оказывается, есть и черные березы. С подобной проблемой столкнулась знаменитая «курица Рассела». У Б. Рассела есть такая притча. В курятнике живет курица. Ежедневно приходит хозяин, приносит ей поклевать зернышек. Курица, естественно, делает отсюда вывод: с появлением хозяина связано появление зернышек. Но вот однажды хозяин является не с зернышком, а с ножом... Это и есть «противоречащий случай»!
Степень вероятности получения истинного вывода на основе популярной индукции зависит от двух важнейших условий: 1) количества обозреваемых случаев; 2) качества признака, т. е. степени его существенности для данного класса предметов.
Однако и это не в состоянии устранить основные недостатки популярной индукции. Один из них состоит в том, что дается простое перечисление случаев повторяемости одного и того же признака и не делается сознательного отбора типичных фактов и их специального анализа. Другой — в том, что обобщение производится на основе простого наблюдения случайно попавшейся совокупности предметов класса и не исследуется причина самого явления. Вот почему наряду со многими верными народными приметами есть немало ложных обобщений, лежащих в основе суеверия, поверий, заклинаний и т. п., — о «пустых ведрах», «черной кошке», «сглазе», «заговоре» и пр.
Научная индукция. Отмеченные выше недостатки популярной индукции преодолеваются так называемой «научной индукцией» (хотя правильно называть ее неполной научной индукцией, так как научной может быть и полная). С ее помощью не просто наблюдаются отдельные случаи, а исследуется природа самого явления и дается ответ на вопрос: «Почему так, а не иначе?» Например, достаточно понять, что ласточки перед дождем летают низко над землей потому, что низко летают мошки, за которыми они охотятся; а те летают низко потому, что перед дождем у них набухают крылышки. Благодаря этому степень вероятности получения истинного вывода в неполной индукции значительно повышается.
Другой пример. В результате популярной индукции было установлено, что металлы при нагревании расширяются. Но все или только некоторые? И лишь молекулярная теория, раскрыв механизм этого расширения, сделала общий вывод, и притом вывод достоверный.
Если в популярной индукции важно обозреть как можно большее число случаев, то для научной индукции это не имеет принципиального значения. Легенда гласит, что Ньютону для открытия фундаментального закона всемирного тяготения достаточно было наблюдать один случай — падение яблока. Это легенда. Но вот факт. Известно, что исходным пунктом для открытия Р. Майером другого фундаментального закона — закона сохранения и превращения энергии послужили наблюдения над цветом крови людей в разных климатических поясах. Открытие многих законов в естественных и общественных науках так или иначе связано с индукцией, зачастую неполной.
Конечно, в разных науках неполная индукция проявляется по-разному. Так, в познании микромира, где действуют преимущественно статистические закономерности, широко используется статистическая индукция. Она нередко применяется в социологических исследованиях: например, при выявлении рейтинга того или иного политического деятеля, вероятности избрания того или иного человека на какой-либо государственный пост и при других опросах общественного мнения. Однако в любой разновидности научной индукции действуют общие закономерности, исследуемые формальной логикой.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
3.13. Что такое индукция?
3.13. Что такое индукция? Вспомним, опосредованные умозаключения делятся на дедуктивные, индуктивные и умозаключения по аналогии. Дедуктивные умозаключения, или силлогизмы, разновидности которых мы рассмотрели выше, дают достоверные выводы. Индуктивное умозаключение,
§ 2. ПОПУЛЯРНАЯ ИНДУКЦИЯ
§ 2. ПОПУЛЯРНАЯ ИНДУКЦИЯ В процессе многовековой деятельности люди наблюдали устойчивую повторяемость многих явлений, которые обобщались и использовались в объяснении наступивших и предсказании будущих событий.Такого рода обобщения связаны с наблюдениями над погодой,
§ 3. НАУЧНАЯ ИНДУКЦИЯ
§ 3. НАУЧНАЯ ИНДУКЦИЯ Научной индукцией называют умозаключение, в котором обобщение строится путем отбора необходимых и исключения случайных обстоятельств.В зависимости от способов исследования различают: (1) индукцию методом отбора (селекции) и (2) индукцию методом
Глава V. Индукция
Глава V. Индукция Другой, кроме дедукции, наиболее общий тип умозаключений — это индукция. В ней заключено глубокое своеобразие, и она находится в тесных взаимоотношениях с дедукцией. В реальной практике мышления ее сущность проявляется тоже в многообразных
2. Полная индукция
2. Полная индукция Полной индукция получается в том случае, если, во-первых, исследованы все элементы класса предметов и, во-вторых, если установлено, что каждому из них принадлежит (или не принадлежит) одно и то же общее свойство (отношение).В простейшем случае это выглядит
Глава V. Индукция
Глава V. Индукция 1. Индукция как тип умозаключения Выразите структуру следующих индуктивных умозаключений в схематической форме и определите характер вывода: «Возьмем, например, исследование Роджера Бэкона о происхождении цветов радуги. Сначала у него, как кажется,
1. Индукция как тип умозаключения
1. Индукция как тип умозаключения Выразите структуру следующих индуктивных умозаключений в схематической форме и определите характер вывода: «Возьмем, например, исследование Роджера Бэкона о происхождении цветов радуги. Сначала у него, как кажется, была мысль связать
§ 6. Математическая индукция
§ 6. Математическая индукция «Но не забываете ли вы, что в математике также имеет место индукция?» – может возразить читатель. «Вы описывали математику как типичную дедуктивную науку, в которой все теоремы являются необходимыми следствиями аксиом. Однако вы ведь не
НЕПОЛНАЯ ИНДУКЦИЯ
НЕПОЛНАЯ ИНДУКЦИЯ Индуктивное умозаключение, результатом которого является общий вывод обо всем классе предметов на основании знания лишь некоторых предметов данного класса, принято называть неполной или популярной индукцией. Например, из того, что инертные газы
5. Ардха Матсиендрасана - Неполная поза Матсиендры 1
5. Ардха Матсиендрасана - Неполная поза Матсиендры 1 Выполнение.Матсиендрой звали великого индийского йога древности. Он имел обыкновение сидеть в этой позе, названной потом его именем Матсиендрасана. Ардха на санскрите означает «половина». Название данной позы
6. Ардха Матсиендрасана - Неполная поза Матсиендры 2
6. Ардха Матсиендрасана - Неполная поза Матсиендры 2 Выполнение.То же, что и в упр. 5, с той разницей, что вытянутая нога подобрана так, что пятка касается другого бедра.Терапевтическое воздействие.Такое же, что и в предыдущей
Полная и неполная индукция
Полная и неполная индукция Если мы переберём всех футболистов сборной России и выясним, что среди них нет одноногих — это будет полная индукция, она же — «индукция перебором».Если же мы изучим одного футболиста, и придём к выводу, что играть с протезом в сборной —
Популярная индукция
Популярная индукция Популярная, она же народная индукция — это индукция через перечисление. Та самая, про которую мы говорили вчера. «Если три моих знакомых еврея хитры, то и все евреи хитры».Популярная индукция — одно из любимых орудий демагогов. Например: Василий
Научная индукция
Научная индукция Научная индукция работает иначе. Научная индукция объясняет свои выводы. Вернёмся к нашему примеру с хитрыми евреями. Научная индукция для этого примера может выглядеть так:«Мозг этих трёх евреев имеет особый отдел мозга, отвечающий за хитрость, и этот
Индукция по простому перечислению
Индукция по простому перечислению Раньше эту ошибку даже разбирали в школах. Примерно так: Учительница: Как полагаете дети, негры глупее белых? Вовочка: Конечно, Марь Иванна! Мы же не знаем ни одного великого негра-учёного или негра-писателя! Учительница: Вовочка, ты
Индукция (Induction)
Индукция (Induction) Вид доказательства, в классическом понимании определяемый как переход от частного к общему, или от фактов к закону. Тем самым противостоит дедукции, которая обычно идет от общего к частному, от принципа к следствиям.Нетрудно догадаться, что индукция,