Глава 13 ТЕОРИЯ ХАОСА: ВЗГЛЯД ЗА КУЛИСЫ

Возможно, эта глава (носящая вдобавок еще и тринадцатый номер) несколько выходит за ставшие уже привычными рамки нашей книги: в ней будут несколько подробнее освещены теоретические основы детерминированного хаоса. О хаосе много говорят и пишут, причем весьма часто публикации в средствах массовой информации оказываются просто бессмысленными; читателю же, заинтересовавшемуся этой тематикой, наверняка хотелось бы заглянуть несколько глубже и узнать, чем же именно занимаются ученые, разрабатывающие теорию хаоса. Начнем мы с простого примера — в нем даже не будет ничего хаотического, — который, однако, поможет нам разобраться в том, с чего начинается теория хаоса. Каждому, наверное, известно, что представляют собой люлька или маятник. В нашем примере речь пойдет о движении некоего «идеального» маятника, на который абсолютно не распространяется, скажем, действие силы трения (например, в подшипниках), а потому наш маятник способен, естественно, раскачиваться бесконечно долго. В математике и теоретической физике такое движение представляется особыми графиками, позволяющими одновременно определять и положение маятника в некоторый заданный момент времени, и его скорость. Взгляните на рис. 13.1: сверху представлен наш маятник (отклонение от вертикальной оси, или амплитуда колебаний, обозначено буквой х), а ниже — соответствующая так называемая фазовая плоскость. Вдоль горизонтальной оси нанесено положение х маятника, а вдоль вертикальной, соответственно, его скорость v.

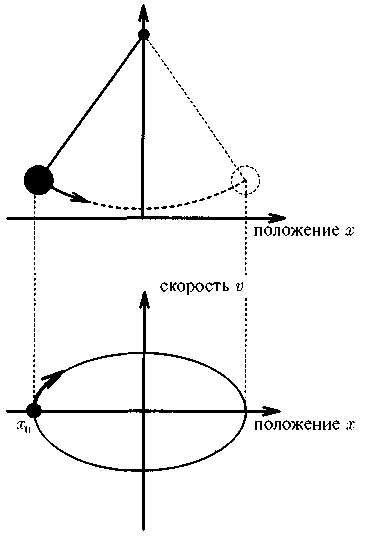
^{Рис. 13.1. Вверху: схема движения маятника; внизу: фазовая плоскость (пояснения даны в тексте)}

Начнем с крайней точки, достигаемой маятником при максимальном отклонении влево. В этой точке скорость маятника равна нулю, и на фазовой плоскости мы обозначим эту точку через x₀. Отсюда маятник, естественно, качнется назад; отклонение при этом уменьшится, а скорость, напротив, возрастет — это дает нам участок кривой, находящийся в левом верхнем квадранте фазовой плоскости. Затем маятник проходит через нижнюю точку своей траектории; здесь отклонение от вертикали равно нулю. Далее отклонение увеличивается, а скорость одновременно снижается, и мы получаем следующий участок кривой — он расположен в правом верхнем квадранте плоскости. Когда маятник достигает крайнего правого положения, скорость вновь падает до нуля; затем отклонение опять уменьшается, а скорость растет, но теперь уже в противоположном начальному направлении, что и отображено на графике нанесением значений скорости на вертикальную ось в нижней части плоскости. Аналогичным описанному образом мы проводим и завершающие этапы построения кривой, получая ее участки для правого и левого нижних квадрантов фазовой плоскости. Маятник продолжает движение, и весь процесс повторяется заново. Точка же, соответствующая на фазовой плоскости физическому положению движущегося маятника, проходит путь, описываемый полученной кривой, которая является, как показано на схеме, эллипсом. Такая замкнутая траектория называется предельным циклом.

Теперь перейдем к случаю движения реального маятника. Через некоторое время после того, как маятник получит начальный толчок, он должен будет остановиться под воздействием силы трения; с течением времени и амплитуда, и скорость маятника неизменно уменьшаются, что в конце концов придает фазовой кривой вид сходящейся к центру спирали (рис. 13.2).

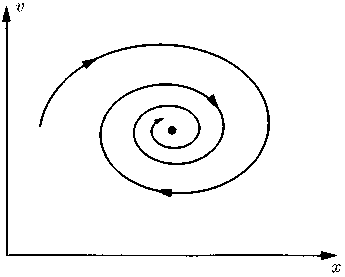
^{Рис. 13.2. Затухающие колебания маятника: траектория сходится к нулевой точке, называемой также фокусом}

Чтобы маятник и в этом случае двигался по траектории, описанной для идеального случая и называемой предельным циклом, необходимо обеспечить постоянное поступление дополнительной энергии (так, бывает, машинально покачивают люльку). Незатухающие колебания маятника характеризуются совершенно определенным временным периодом, который можно замерить. В случае же затухающего движения свободно качающийся маятник, к сожалению, со временем теряет скорость и переходит в состояние покоя. Однако если маятник соединить с механизмом, который снова и снова «подталкивал» бы его, то мы получим нечто вроде часов; в действительности такая конструкция применялась многократно и в различных вариантах — сначала в чисто механическом исполнении, а затем в сочетании с кварцевым резонатором.

Маятник можно рассматривать как прототип колебательных процессов в различных областях; более того, бытует мнение, что именно такими предельными циклами или составленными из них кривыми задаются наиболее интересные траектории в фазовой плоскости — или в «фазовых пространствах» большей размерности. Кроме того, метеорологу Эдварду Лоренцу удалось сделать потрясающее открытие: исследуя динамику жидкости, он обнаружил, что уже в трехмерных моделях могут появляться совершенно поразительные траектории; один из примеров показан на рис. 13.3. Так был открыт хаос, а говоря точнее — открыт заново; в двенадцатой главе мы уже упоминали о том, что знаменитый французский математик Анри Пуанкаре занимался изучением разных типов хаотического движения еще на рубеже веков.

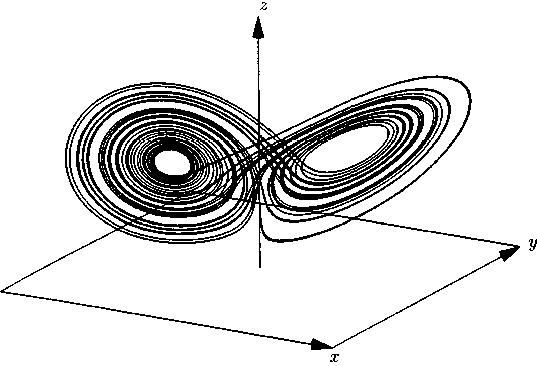
^{Рис. 13.3. Аттрактор Лоренца. Изображающая точка траектории сначала совершает вращательное движение в одной области пространства, а затем вдруг' совершенно неожиданно перескакивает в другую область и некоторое время продолжает движение там; по истечении некоторого времени происходит новый «скачок» — обратно в исходную область — и т.д. Хотя описанное движение и удовлетворяет детерминистским уравнениям, прыжки выглядят как чисто случайные}

Как показал мой бывший докторант Готтфрид Майер-Кресс, хаотическое движение весьма просто реализуется с помощью конструкции, называемой колесом Пола. Маятник пружиной соединен с рычагом, совершающим вследствие вращения двигателя периодическое возвратно-поступательное движение. Когда сцепление невелико, движение рычага вызывает вынужденные колебания маятника. Таким образом возникают траектории, подобные той, что показана на рис. 13.1. Однако стоит увеличить сцепление, как картина внезапно меняется; обнаруживается некая «точка перехода», изменяющая период колебания маятника: чтобы вернуться назад в исходное положение, маятнику теперь требуется в два раза больше времени. После нескольких подобных промежуточных стадий, вызываемых повышением сцепления, движение маятника становится уже совершенно неупорядоченным, или хаотическим. Итак, очевидно, что порождение хаоса — задача не из сложных.

Естественно, математики и физики-теоретики задумывались о том, каким образом можно характеризовать подобные хаотические траектории более точно. В первую очередь остановимся на феномене, который я называю «эффектом лезвия» (см. рис. 12.2); в научной же терминологии этот феномен известен как чувствительность к исходным условиям. Рассмотрим две траектории, поначалу проходящие в непосредственной близости друг от друга в фазовом пространстве. Как можно убедиться, они очень быстро расходятся — расстояние между ними увеличивается по экспоненте. Соответствующую кривую, описывающую скорость увеличения расстояния, называют еще экспонентой Ляпунова.

Следующим характерным свойством хаотических траекторий является их самоподобие. Продемонстрируем этот феномен на примере кривой, построенной шведским математиком Хельге фон Кохом еще в 1904 году (рис. 13.4).

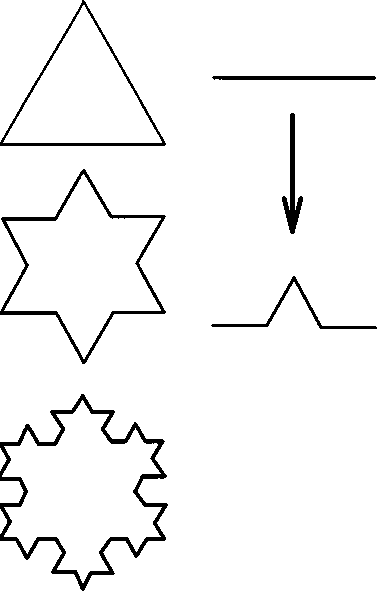
^{Рис. 13.4. Пример фрактальной кривой — кривая Коха. Для получения такой кривой на средней трети каждой из сторон равностороннего треугольника следует построить новый равносторонний треугольник; процесс может быть продолжен до бесконечности}

Помимо прочего, феномен этот демонстрирует одно любопытное следствие: невозможно со всей определенностью сказать, при каком увеличении мы рассматриваем семейство таких кривых (рис. 13.5): они выглядят одинаково в самых различных масштабах. Наконец, мы можем представить себе хаотические траектории как клубок шерсти, сквозь который снова и снова продевается нить. Шерсть в таком клубке заполняет пространство не полностью, а лишь частично; в этом случае говорят о фрактальной, т.е. дробной размерности кривой.

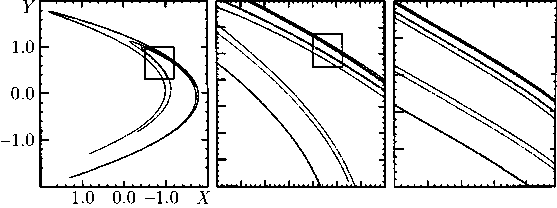
^{Рис. 13.5. Самоподобие на примере хаотического аттрактора: при увеличении какой-либо подобласти заметного изменения картины не происходит, вследствие чего невозможно определить, с каким увеличением представлен аттрактор}

Надеясь, что читателя не слишком сильно отпугивает терминология, попытаюсь ввести еще одно важное понятие — аттрактор. На примере затухающего движения маятника мы видели, как кривая, описывающая его траекторию, приближается к нулевой точке. Точка эта в некотором смысле притягивает к себе кривую или, иными словами, становится аттрактором. В случае хаотического движения состояние покоя не наступает никогда, однако и здесь мы можем говорить о существовании аттрактора. Допустим, некая траектория начинается где-то вблизи от так называемого аттрактора; войдя в данную пространственную область — в область притяжения — кривая уже никогда больше не покинет ее. Здесь кривая и будет кружить вечно; однако — как уже было упомянуто — так никогда и не сумев заполнить собою всего доступного ей пространства.

Поскольку характеристики подобных кривых не особенно наглядны при рассмотрении в трех или более измерениях, предпринимались попытки описать такие траектории, использовав пространства меньшей размерности. Очень важный вклад в эти исследования внес Пуанкаре. На рис. 13.6 представлено отображение, названное его именем.

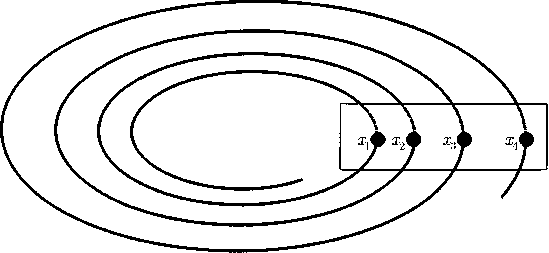
^{Рис. 13.6. Построение отображения Пуанкаре. В предлагаемом примере траектории движутся в трехмерном пространстве и пробивают при этом вложенную плоскость сечения. Координаты точек пробива образуют последовательность х1, x2, …}

С помощью отображения Пуанкаре стало возможно представить непрерывную кривую в виде последовательности отдельных, т.е. дискретных, точек х₁, x₂, ... Математики и физики-теоретики, кстати, склонны при случае к разного рода шуткам и играм: в конце концов такие шутки часто оказываются весьма полезны и в высшей степени продуктивны и поучительны, так как способствуют углублению взглядов на имеющие место закономерности. Одной из подобных забав казалось поначалу выдвижение в качестве постулата предположения о наличии зависимости между последовательными точками х_п. Например, координата точки на пятом витке кривой ровно в ? раз больше, чем координата точки на четвертом витке. Правда, это еще не дает нам возможности сделать ни одного хоть сколько-нибудь интересного заключения (рис. 13.7).

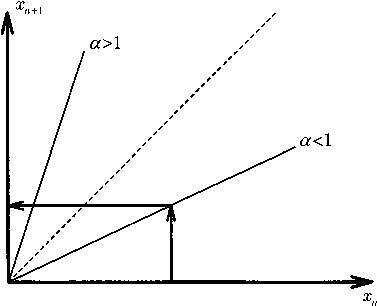
^{Рис. 13.7. Схематическое описание зависимости между координатой хп точки, достигнутой кривой на n-м витке, и координатой следующей за ней точкой xn+i, n = — 1, 2, 3, . ... Если эта зависимость линейна, как в данном случае, то не происходит ничего примечательного. При ? < 1 точки сходятся к некоторой нулевой точке, при ? > 1 — расходятся в бесконечность, в чем легко убедиться посредством итераций предлагаемого отображения}

Если ? < 1, то точки в конечном счете сходятся к нулевой точке; в остальных случаях, т.е. при ? > 1, точки расходятся в бесконечность. При ? = 1 все точки совпадают. Однако рассматривая следующие по степени сложности кривые — например параболическую зависимость х_п+1 от х_п — мы вдруг сталкиваемся с массой удивительнейших явлений.

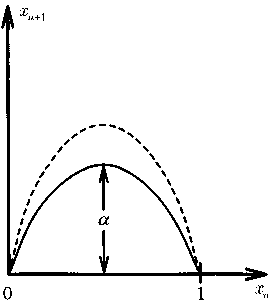
^{Рис. 13.8. Простейшая после линейной параболическая зависимость координаты хп + 1 от предыдущего значения хn}

При увеличении высоты ? (рис. 13.8) возникает совершенно иная последовательность значений х_п; несколько первых элементов этой последовательности представлены на рис. 13.9.

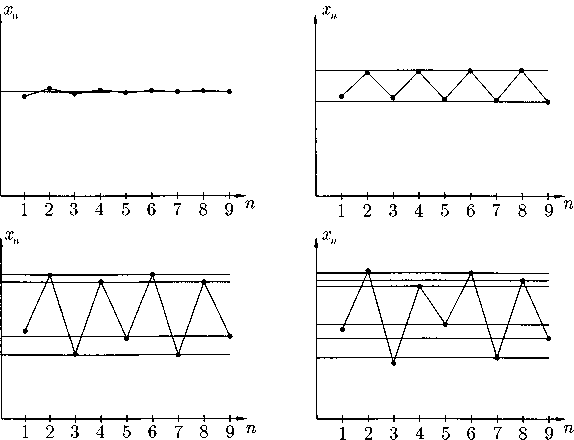
^{Рис. 13.9. Динамика изменений значения хп в зависимости от высоты ? (см. рис. 13.8); при малых ? значение хп остается постоянным. Если же ? увеличивается, то при превышении некоторого критического значения возникает циклическое движение, при котором период достижения исходного состояния удваивается (сравните с первой частью рисунка). При дальнейшем увеличении ? продолжительность периода удваивается еще раз (т. е. теперь она превышает начальную в 4 раза), затем — с очередным повышением величины ? — вновь удваивается (и отличается от начальной уже в 8 раз) и т. д. В таких сериях обнаружен ряд любопытнейших самоподобных свойств}

При вполне определенных значениях ? период, необходимый кривой для достижения исходной величины х_п, удваивается; в этом случае можно говорить о последовательности удвоений периода. При некоторой предельной величине ? эти удвоения периода переходят в совершенно неупорядоченную последовательность значений х_п, т.е. перед нами снова проявление хаотического поведения. Зигфрид Гроссман и С. Томе обнаружили здесь в высшей степени интересные общие закономерности; однако мы, похоже, углубляемся в излишние подробности — заинтересованных читателей я отсылаю к специальной литературе. Впрочем, добавлю еще, что проиллюстрированное на рис. 13.8 уравнение называется логистическим и применяется для описания неупорядоченных изменений, происходящих, например, в популяциях насекомых (о них уже упоминалось в предыдущей главе). Удвоение периода — это лишь один из путей к хаосу. Одно время, правда, считалось, что этот путь — единственный; однако затем были обнаружены и другие пути, и сегодня нам известно, что существует бесконечное множество различных способов достижения хаотического состояния — например, изменение какого-либо из параметров безобидного на первый взгляд эксперимента.